An Equation of the Line Normal to the Graph of Y=x^3+3x^2+7x-1 at the Point Where X=-1

3. Derivatives

3.8 Absolute Specialization

Learning Objectives

Find the derivative of a complex function away using tacit differentiation.
Use understood differentiation to determine the equation of a tangent line.

We have already studied how to find equations of tangent lines to functions and the rate of change of a function at a specific item. Altogether these cases we had the explicit equation for the operate and differentiated these functions explicitly. Guess rather that we want to determine the equation of a tangent telephone line to an arbitrary curve or the rate of change of an absolute bend at a breaker point. In this section, we solve these problems by finding the derivatives of functions that define $y$ implicitly in terms of $x$ .

Implicit Differentiation

In all but discussions of math, if the dependent changeable $y$ is a go of the independent variable $x$ , we express mail $y$ in footing of $x$ . If this is the case, we say that $y$ is an explicit go of $x$ . For good example, when we write the equation $y=x^2+1$ , we are defining $y$ expressly in price of $x$ . But then, if the relationship between the function $y$ and the variable $x$ is overt by an equation where $y$ is non verbalised entirely in damage of $x$ , we enunciat that the par defines $y$ implicitly in terms of $x$ . E.g., the equation $y-x^2=1$ defines the function $y=x^2+1$ implicitly.

Implicit differentiation allows us to find slopes of tangents to curves that are clear not functions (they fail the vertical line of business trial). We are using the theme that portions of $y$ are functions that satisfy the given equality, but that $y$ is not actually a function of $x$ .

In general, an equation defines a function implicitly if the part satisfies that equality. An equation may define many different functions implicitly. For example, the functions

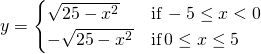$y=\sqrt{25-x^2}$ , $y = -\sqrt{25-x^2}$ , and $y=\begin{cases} \sqrt{25-x^2} & \text{if} \, -5 \le x < 0 \\ -\sqrt{25-x^2} & \text{if} \, 0 \le x \le 5 \end{cases}$ , which are illustrated in (Figure), are just three of the umteen functions defined implicitly aside the equation $x^2+y^2=25$ .

If we want to find the slope of the line tangent to the chart of $x^2+y^2=25$ at the dot $(3,4)$ , we could evaluate the derivative of the function $y=\sqrt{25-x^2}$ at $x=3$ . On the other hand, if we desire the slope of the tan line at the point $(3,-4)$ , we could use the derivative of $y=−\sqrt{25-x^2}$ . However, it is not forever easy to solve for a function settled implicitly by an equation. Fortuitously, the technique of implicit differentiation allows us to find the first derivative of an implicitly defined function without ever solving for the function explicitly. The process of finding $\frac{dy}{dx}$ using implicit differentiation is described in the following job-resolution strategy.

Using Unspoken Differentiation

Assuming that $y$ is defined implicitly past the equation $x^2+y^2=25$ , chance $\frac{dy}{dx}$ .

Solution

Follow the steps in the problem-resolution scheme.

$\begin{array}{llll} \frac{d}{dx}(x^2+y^2) = \frac{d}{dx}(25) & & & \text{Step 1. Differentiate both sides of the equation.} \\ \frac{d}{dx}(x^2)+\frac{d}{dx}(y^2) = 0 & & & \begin{array}{l}\text{Step 1.1. Use the sum rule on the left.} \\ \text{On the right,} \, \frac{d}{dx}(25)=0. \end{array} \\ 2x+2y\frac{dy}{dx} = 0 & & & \begin{array}{l}\text{Step 1.2. Take the derivatives, so} \, \frac{d}{dx}(x^2)=2x \\ \text{and} \, \frac{d}{dx}(y^2)=2y\frac{dy}{dx}. \end{array} \\ 2y\frac{dy}{dx} = -2x & & & \begin{array}{l}\text{Step 2. Keep the terms with} \, \frac{dy}{dx} \, \text{on the left.} \\ \text{Move the remaining terms to the right.} \end{array} \\ \frac{dy}{dx} = -\frac{x}{y} & & & \begin{array}{l}\text{Step 4. Divide both sides of the equation by} \\ 2y. \, \text{(Step 3 does not apply in this case.)} \end{array} \end{array}$

Using Unvoiced Differentiation and the Product Prescript

Forward that $y$ is defined implicitly by the equation $x^3 \sin y+y=4x+3$ , find $\frac{dy}{dx}$ .

Solution

$\begin{array}{llll}\frac{d}{dx}(x^3 \sin y+y) = \frac{d}{dx}(4x+3) & & & \text{Step 1: Differentiate both sides of the equation.} \\ \frac{d}{dx}(x^3 \sin y)+\frac{d}{dx}(y) = 4 & & & \begin{array}{l}\text{Step 1.1: Apply the sum rule on the left.} \\ \text{On the right,} \, \frac{d}{dx}(4x+3)=4. \end{array} \\ (\frac{d}{dx}(x^3) \cdot \sin y+\frac{d}{dx}(\sin y) \cdot x^3) + \frac{dy}{dx} = 4 & & & \begin{array}{l}\text{Step 1.2: Use the product rule to find} \\ \frac{d}{dx}(x^3 \sin y). \, \text{Observe that} \, \frac{d}{dx}(y)=\frac{dy}{dx}. \end{array} \\ 3x^2 \sin y+(\cos y\frac{dy}{dx}) \cdot x^3 + \frac{dy}{dx} = 4 & & & \begin{array}{l}\text{Step 1.3: We know} \, \frac{d}{dx}(x^3)=3x^2. \, \text{Use the} \\ \text{chain rule to obtain} \, \frac{d}{dx}(\sin y)= \cos y\frac{dy}{dx}. \end{array} \\ x^3 \cos y\frac{dy}{dx}+\frac{dy}{dx} = 4-3x^2 \sin y & & & \begin{array}{l}\text{Step 2: Keep all terms containing} \, \frac{dy}{dx} \, \text{on the} \\ \text{left. Move all other terms to the right.} \end{array} \\ \frac{dy}{dx}(x^3 \cos y+1) = 4-3x^2 \sin y & & & \text{Step 3: Factor out} \, \frac{dy}{dx} \, \text{on the left.} \\ \frac{dy}{dx} = \large \frac{4-3x^2 \sin y}{x^3 \cos y+1} & & & \begin{array}{l}\text{Step 4: Solve for} \, \frac{dy}{dx} \, \text{by dividing both sides of} \\ \text{the equation by} \, x^3 \cos y+1. \end{array} \end{array}$

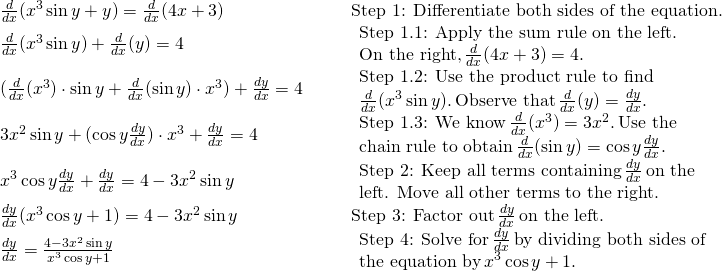
Using Implicit Differentiation to Find a Second Derivative instrument

Find $\frac{d^2 y}{dx^2}$ if $x^2+y^2=25$ .

Solution

In (Figure), we showed that $\frac{dy}{dx}=-\frac{x}{y}$ . We can involve the derivative of both sides of this equating to find $\frac{d^2 y}{dx^2}$ .

$\begin{array}{lllll} \frac{d^2 y}{dx^2} & =\large \frac{d}{dx}(-\frac{x}{y}) & & & \text{Differentiate both sides of} \, \frac{dy}{dx}=-\frac{x}{y}. \\ & = \large -\frac{(1 \cdot y-x\frac{dy}{dx})}{y^2} & & & \text{Use the quotient rule to find} \, \frac{d}{dx}(-\frac{x}{y}). \\ & = \large \frac{−y+x\frac{dy}{dx}}{y^2} & & & \text{Simplify.} \\ & = \large \frac{−y+x(-\frac{x}{y})}{y^2} & & & \text{Substitute} \, \frac{dy}{dx}=-\frac{x}{y}. \\ & = \large \frac{−y^2-x^2}{y^3} & & & \text{Simplify.} \end{array}$

At this dot we have found an expression for $\frac{d^2 y}{dx^2}$ . If we choose, we can simplify the expression further by recalling that $x^2+y^2=25$ and making this substitution in the numerator to obtain $\frac{d^2 y}{dx^2}=-\frac{25}{y^3}$ .

Find $\frac{dy}{dx}$ for $y$ defined implicitly past the equation $4x^5+ \tan y=y^2+5x$ .

Solution

$\frac{dy}{dx}=\large \frac{5-20x^4}{\sec^2 y-2y}$

Finding Tan Lines Implicitly

Immediately that we induce seen the technique of implicit differentiation, we can apply it to the problem of finding equations of tangent lines to curves delineated by equations.

Finding a Tangent Line of merchandise to a Circle

Find the equation of the line tangent to the curve $x^2+y^2=25$ at the point $(3,-4)$ .

Finding the Equation of the Tangent Line to a Curve ball

Encounte the equation of the line tangent to the graph of $y^3+x^3-3xy=0$ at the point $(\frac{3}{2},\frac{3}{2})$ ((Figure)). This curve is known as the folium (or leaf) of Descartes.

Solution

Begin by finding $\frac{dy}{dx}.$

$\begin{array}{l} \frac{d}{dx}(y^3+x^3-3xy) = \frac{d}{dx}(0) \\ \\ 3y^2\frac{dy}{dx}+3x^2-(3y+3x\frac{dy}{dx}) = 0 \\ \\ \frac{dy}{dx} = \frac{3y-3x^2}{3y^2-3x}. \\ \\ \end{array}$

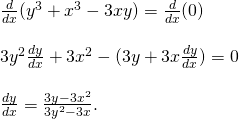
Next, substitute $(\frac{3}{2},\frac{3}{2})$ into $\frac{dy}{dx}=\frac{3y-3x^2}{3y^2-3x}$ to find the gradient of the tangent line:

$\frac{dy}{dx}|_{(\frac{3}{2},\frac{3}{2})}=-1$ .

At long last, second-string into the bespeak-gradient equation of the stoc and clear for $y$ to incur

$y=−x+3$ .

Applying Implicit Differentiation

Observe the equation of the line tangent to the hyperbola $x^2-y^2=16$ at the point $(5,3)$ .

Root

$y=\frac{5}{3}x-\frac{16}{3}$

Key Concepts

We use unvoiced differentiation to find derivatives of implicitly defined functions (functions delimited by equations).
By exploitation implicit differentiation, we can find the equation of a tangent personal credit line to the graph of a curve.

For the chase exercises, use implicit differentiation to find $\frac{dy}{dx}$ .

1. $x^2-y^2=4$

2. $6x^2+3y^2=12$

Solution

$\frac{dy}{dx}=\frac{-2x}{y}$

3. $x^2 y=y-7$

4. $3x^3+9xy^2=5x^3$

Solution

$\frac{dy}{dx}=\frac{x}{3y}-\frac{y}{2x}$

5. $xy- \cos (xy)=1$

6. $y\sqrt{x+4}=xy+8$

Solution

$\frac{dy}{dx}=\large \frac{y-\frac{y}{2\sqrt{x+4}}}{\sqrt{x+4}-x}$

7. $−xy-2=\frac{x}{7}$

8. $y \sin(xy)=y^2+2$

Answer

$\frac{dy}{dx}=\large \frac{y^2 \cos(xy)}{2y- \sin(xy)-xy \cos xy}$

9. $(xy)^2+3x=y^2$

10. $x^3 y+xy^3=-8$

[reveal-answer q="608460″]Picture Solvent[/reveal-answer]
[hidden-resolution a="608460″]
$\frac{dy}{dx}=\large \frac{-3x^2 y-y^3}{x^3+3xy^2}$

For the following exercises, find the equivalence of the tangent line to the graph of the given equation at the indicated point. Use a calculator or computer software to graph the function and the tangent line.

11. [T] $x^4 y-xy^3=-2, \, (-1,-1)$

13. [T] $\tan (xy)=y, \, (\frac{\pi}{4},1)$

15. [T] $\frac{x}{y}+5x-7=-\frac{3}{4}y, \, (1,2)$

17. [T] The graph of a folium of Descartes with equation $2x^3+2y^3-9xy=0$ is given in the following graph.

A folium is graphed which has equation 2x3 + 2y3 – 9xy = 0. It crosses over itself at (0, 0).

Find the equation of the tangent line at the indicate 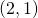$(2,1)$ . Graph the tan line on with the folium.
Find the equation of the normal melody to the tangent line in a. at the point $(2,1)$ .

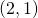18.For the equation $x^2+2xy-3y^2=0$ ,

Find the par of the normal to the tangent credit line at the point $(1,1)$ .
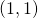At what other sharpen does the sane line in a. intersect the graph of the equation?

Solution

a. $y=−x+2$
b. $(3,-1)$

19.Find every points along the chart of $y^3-27y=x^2-90$ at which the tangent line is standing.

Solution

a. $(\pm \sqrt{7},0)$
b. Side is -2 at some intercepts
c. They are parallel since the slope is the same at both intercepts.

21.Find the equation of the tangent line to the graph of the equation $\sin^{-1} x+\sin^{-1} y=\frac{\pi}{6}$ at the point $(0,\frac{1}{2})$ .

22.Find the equation of the tangent line to the graphical record of the equality $\tan^{-1}(x+y)=x^2+\frac{\pi}{4}$ at the maneuver $(0,1)$ .

Solution

$y=−x+1$

Solution

a. -0.5926
b. When $81 is spent on labor and $16 is worn out on Das Kapital, the amount spent on capital is decreasing by $0.5926 per $1 spent on labor.

For the following exercises, consider a closed rectangular box with a square base with side $x$ and height $y$ .

27.Find an equality for the opencast area of the rectangular box, $S(x,y)$ .

28.If the surface arena of the rectangular box is 78 angular feet, find $\frac{dy}{dx}$ when $x=3$ feet and $y=5$ feet.

Solution

$\frac{dy}{dx}=-2.67$

For the following exercises, use implicit differentiation to determine $y^{\prime}$ . Does the answer correspond with the formulas we have previously determined?

29. $x= \sin y$

30. $x= \cos y$

Solution

$y^{\prime}=-\frac{1}{\sqrt{1-x^2}}$

31. $x= \tan y$

An Equation of the Line Normal to the Graph of Y=x^3+3x^2+7x-1 at the Point Where X=-1

Source: https://opentextbc.ca/calculusv1openstax/chapter/implicit-differentiation/

An Equation of the Line Normal to the Graph of Y=x^3+3x^2+7x-1 at the Point Where X=-1

3.8 Absolute Specialization

Learning Objectives

Implicit Differentiation

Using Unspoken Differentiation

Solution

Using Unvoiced Differentiation and the Product Prescript

Solution

Using Implicit Differentiation to Find a Second Derivative instrument

Solution

Solution

Finding Tan Lines Implicitly

Finding a Tangent Line of merchandise to a Circle

Finding the Equation of the Tangent Line to a Curve ball

Solution

Applying Implicit Differentiation

Root

Key Concepts

Solution

Solution

Solution

Answer

Solution

Solution

Solution

Solution

Solution

Solution

0 Response to "An Equation of the Line Normal to the Graph of Y=x^3+3x^2+7x-1 at the Point Where X=-1"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel